Phase Shift Calculator: A Comprehensive Guide You Should Read

Are you finding it challenging to phase shift calculator, phase angle, or phase difference of trigonometric functions? If yes, you need to keep reading this article.

The phase shift calculator is pretty essential in the PCB reverse engineering, science, and mathematics world.

But, using it could get very tricky with the tons of formulas and technical terms that come with it, like:

• Cutoff Frequencies
• Sampling Frequency
• Resonance Frequency
• Phase Step A

Luckily, we wrote this simple but comprehensive guide to make things easier for you. This article will tell you everything you need to know about the calculating phase shift and the different formulas surrounding it.

So, let’s get started!

1. What Is the Phase Shift of a Function?

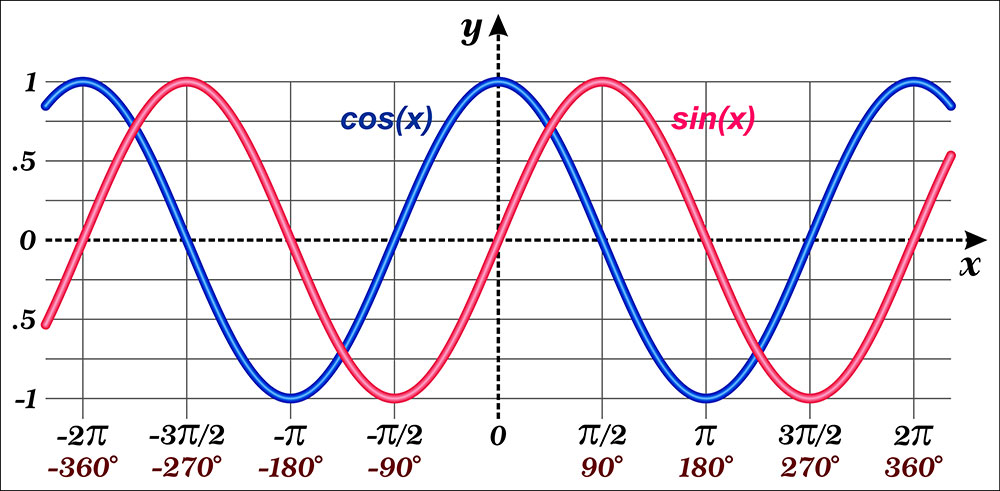
The phase shift of a function refers to the different points in the cycle of two signals—in a position at a given time. So, the functions we’ll be looking at here are trigonometric functions, especially the sine and cosine.

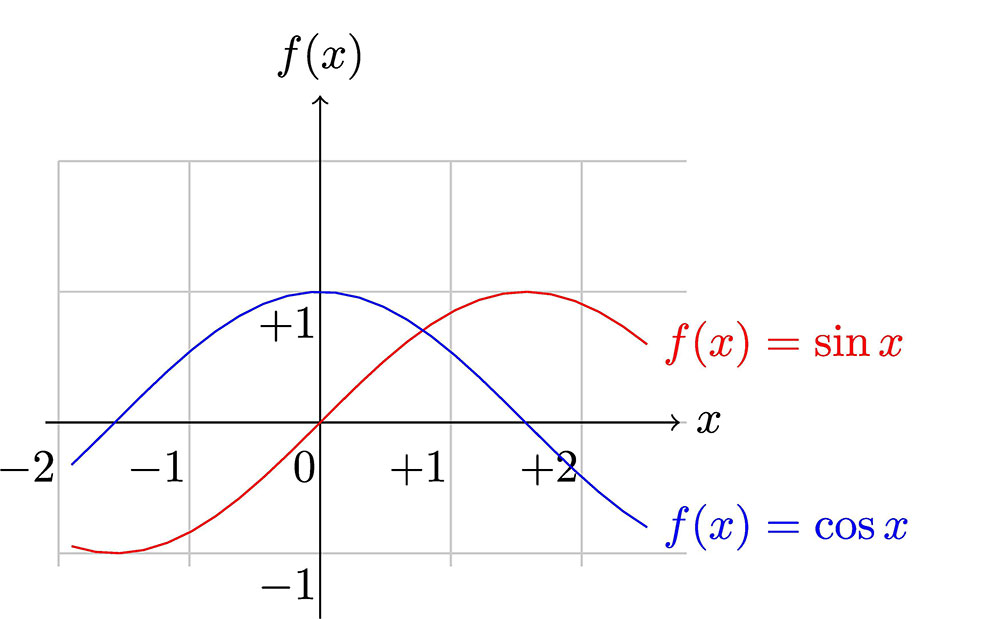
Plotting of Sin(x) and Cos(x) functions.

Also, we’ll focus on the amplitude, period, phase shift, and vertical shift. But, before we go deeper, let’s examine where these notions appear on a graph.

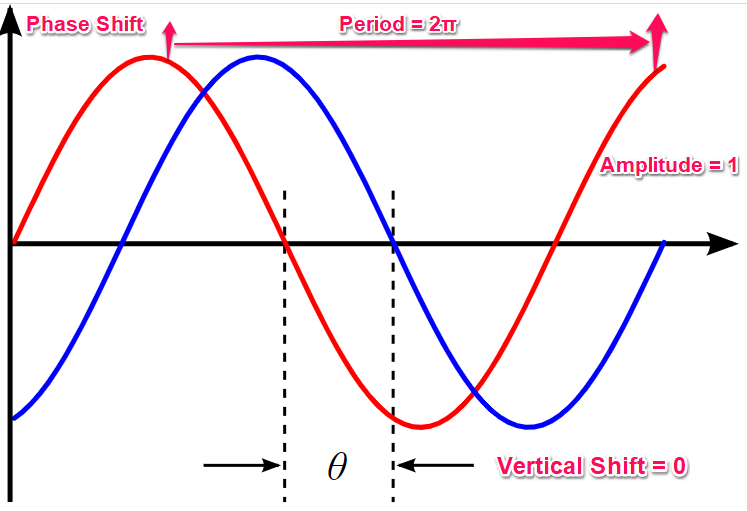
Notion’s graph showing the positions of Phase shift, Period, Amplitude, and Vertical shift

You use the degree phase shift formula (or phase shift equation) to write such functions.

For Sine:

f(x) = A x sin (Bx - C) + D

For cosine:

f(x) = A x cos (Bx - C) + D

Three Phase Sine wave

For A, B, C, D, use arbitrary real numbers and non-zero with A and B (so this would be a trigonometric function). You can use these four numbers to determine the amplitude period phase shift and vertical shift.

Sine Wave generator

There are additional phase shifts for more complex calculations, but we'll stick to the basics for this article.

2. How to Calculate the Phase Shift?

So, let’s look at the notions mentioned earlier and calculate phase shifts using the equation. If you recall, the ideas or aspects for trigonometric functions include amplitude, period, phase shift, and vertical shift.

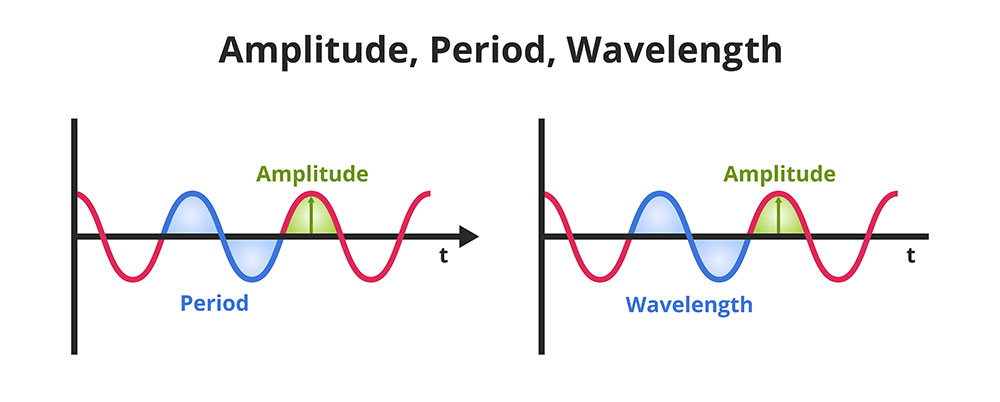
Diagram showing Amplitude, Period, and Wavelength

• Amplitude

Amplitude indicates the movement of values from the centerline of the graph to the peak (top) and the trough (bottom). For a simple sine or cosine function, you can set the value at 1 and the centerline at 0.

Therefore, the function’s value will range from -1 to 1. Basically, the amplitude is A in the phase shift equation.

• Period

Plotted graph of Sine and Cosine

The sine and cosine functions both have periods, but what is the period?  The period moves from one point to the next matching point—the peak of the function—the period of a phase shift = 2π/B.

• Phase Shift

The phase shift, also known as horizontal shift, refers to how far the function can move horizontally from its original position. The phase shift in the original phase difference calculation is C.

• Vertical Shift

The vertical shift refers to how far the function can vertically move from its original position. The D in the phase shift equation is the vertical shift.

In a nutshell;

We can have the equation:

Y= A sin (B(x + C)) + D

Where:

• A= Amplitude
• 2π/B =period
• C = Phase shift
• D = Vertical shift

Here’s an example of this formula in action:

2 sin (4(x 0.5)) + 3

Where:

• Amplitude (A) = 2
• Period (2π/B) = 2π/4 = π/2
• Phase shift (C) = 0.5 to the right
• Vertical shift (D) = 3

Here’s the graph for a visual interpretation:

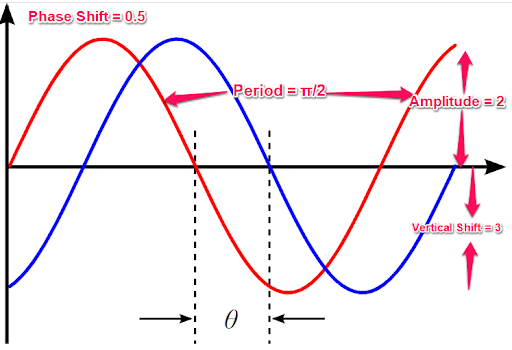
Notion graph for the above equation

 Also, here’s an explanation:

•     The amplitude tells us the function on the graph will be 2 times taller than its original height. So, the amplitude = 2
•     Usually, the period is 2π, but in this equation, the period is shorter by 4 in 4x. Hence, the period = π/2
•     The 0.5 here means the function is shifted 0.5 to the right. So, the phase shift = 0.5
•     Finally, the D tells us the centerline is y = +3. Thus, the vertical shift = 3

3. Using Phase Shift Calculator to Solve Examples

Here, we’ll be using a phase shift calculator to find the phase shift of a tangent. Before we start solving, here’s a picture of the phase shift calculator we’ll be working with:

Calculator for Tangent Phase Shift

How to Find the Phase Shift of a Tangent

The phase shift of the tangent function is a different ball game. Fortunately, we are here to make things easy.

Take a look at this example to understand this frequency term:

Y = tan (x + 60)

So, let’s look at the phase shift equation for trigonometric functions in the form:

Y = a tan(b(x+c))+d

We’ve already discussed that:

• Amplitude = a
• Period = π/b
• Phase shift = −c/b
• Vertical shift = d

So, using the example: Y = tan(x+60)

• Amplitude (see below)
• period =π/c
• period= 180/1 = 180
• Phase shift=−c/b=−60/1=60

This equation is similar to the graph of y = tan(x), which turned 60 degrees in the negative x-direction.

Vertical shift=d=0 (there is no vertical shift)

Plus, there’s no measurement for the amplitude of the tangent function because tan(x) is undefined.

Graphs: of Y = tan(x) and Y = tan(x+60)

How to Graph Trig Functions with Phase Shift?

Trigonometric system plotting on a graph

Basically, trig functions are angles. Hence, they include sine, cosine, tangent, or cotangent. Finding the phase shift is a significant aspect to solve when evaluating trig functions.

So, let’s look at three easy steps to help you graph a function with a phase shift.

For example, if you have y = sin (2x - 4) + 6, here’s what you have to do:

First, it would help if you wrote your equation in the trig functions standard form. The standard form is:

Y = A sin (Bx -C) + D

In this case, the equation is already in standard form, so there’s no need to rewrite it.

Second, label all your values (A, B, C, and D). When you compare the example to the standard function, you can see that A = 1, B = 2. C = 4, and D = 6.

The last step is calculating the phase shift. Again, use the formula from the standard form, C/B, to get the phase shift. Then, insert the values for C and B, and the answer you get is the value for the phase shift.

4. Are Horizontal and Phase Shift the Same?

Yes, the horizontal and phase shift are the same thing. So, you can get the horizontal shift by calculating the changes of the x-value. If it is positive, it goes to the right; if it’s negative, it goes to the left. This horizontal shift is also known as phase shift (especially in mathematics).

5. Phase Shift Calculator

The phase shift calculator uses a wide frequency range and time difference delay to calculate the phase shift or angle.

Final Words

Now, you’ve got a more comprehensive and more precise picture of the Phrase shift calculator and its functions like:

• Circuit for phase angles
• Low-pass filter

Nonetheless;

Remember, there are four aspects of getting the phase shift of a function. So, it’s expedient that you understand every calculation pointed out in this article. That way, you.

In closing, we believe this article will hit all the right spots and help you out—with your Phase shift calculations.

But, if you need more information, feel free to contact us.